Mathematical Formulation of Shells in 4D 

Step 1: 3D Model

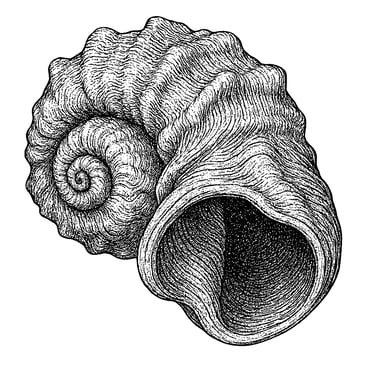
First, let’s see how a helicoidal shell is modeled.
A common model for a shell is a logarithmic helicoidal surface, defined by a parametrization such as:

Where:

• u is the parameter that controls the logarithmic expansion (the shell’s growth),

• v is the angular parameter (like the “turn” of the spiral),

• a,b,c,d are constants controlling the shape (radius, expansion, height per turn, etc.).

Step 2: Extension to 4 Dimensions

To move into 4D, we must add a fourth coordinate w(u,v).
This new coordinate can be:

• Geometrically significant (e.g., a physical property),

• An additional artificial dimension (like evolution over time), or one independent of u, v.

Option 1: Shell Rotating in the Fourth Dimension

• (w,v) adds an oscillatory motion, as if the shell were “spinning” in the fourth dimension:

— time as the fourth dimension (animation)Here, w=t is always time, and the rest of the figure rotates as t increases: